zadania dla Keiry b.: zadania dla Keiry: 1. jakie reszty moze dawac kwadrat liczby calkowitej przy dzieleniu przez 3? 4? 5? 2. znalezc wszystkie liczby pierwsze p,takie ze 4p²+1 oraz 6p²+1 tez sa pierwsze

Keira: Ojeju Chcesz mnie zamęczyć no dobra...spróbuję

Keira: 1 zad. k∊C Mamy trzy przypadki: 3k (l. podzielna przez 3), 3k + 1, 3k + 2 −−− liczby niepodzielne przez 3

3k2
	= 3k2 r0
3

(3k + 1)2		1
	= 3k2 + 2k +		r1
3		3

(3k + 2)2		1
	= 3k2 + 4k + 1		r1
3		3

Zatem przy dzieleniu przez 3 kwadrat liczby calkowitej daje resztę 0 lub 1. Dobrze?

b.: dobrze

Keira: to z 4 i 5 analogicznie? to juz zrobie na kartce, bo pisanie tutaj zajmuje troche czasu

b.: zgadza sie, analogicznie, ok, podaj tylko mozliwe reszty

Keira: Przy 4 − także r 0 lub 1

b.: zgadza sie

Keira: przy 5 − r 0, 1, lub 4

Eta: Witam Wszystkich Dorzucę kilka zadań przeznaczonych dla Keira zad.1/Wyznacz wszystkie liczby naturalne n dla których liczba 2ⁿ+1 jest kwadratem liczby naturalnej. zad.2/ Wyznacz wszystkie liczby pierwsze p, q,r spełniających równanie: pq−19r= 1995 Powodzenia, pozdrawiam

b.: zgadza sie, tylko 0,1 i 4 to jest dosc ciekawa wlasnosc kwadratow, ze nie moga one dawac zupelnie dowolnych reszt z dzielenia, a tylko niektore −− czasami to sie przydaje w zadaniach

Keira: tak, tak, *i 4

Eta: Keira Nie masz ochoty rozwiązać zadań podanych przeze mnie?

b.: powtorzylem to 0,1,4 bez specjalnego zastanowienia, tylko dlatego, ze Eta napisala post na nieco inny temat tutaj wydaje mi sie lepsze Twoje ,,lub'', tak jak w jednym z poprzednich zdan: Zatem przy dzieleniu przez 3 kwadrat liczby calkowitej daje resztę 0 lub 1. Chociaz mozna by tez napisac: Mozliwe reszty ... to 0,1 i 4. Tak to bywa, jak sie nie pisze pelnymi zdaniami (to sa tylko luzne stwierdzenia, nie bierz do siebie, trudno zeby wszystko wklepywac pelnymi zdaniami itp.) @Eta: ale ja popedzasz

Keira: No własnie też tak potem stwierdziłam, że może być i tak i tak, zależnie od zdania. Eta − mam twoje zadanka i będę robić, ale póki co inna robota mnie wezwała Pozdrawiam!

Eta: ok

b.: @Eta: to taki sposob cytowania zwracania sie do kogos = do Ety: to taki sposob cytowania zwracania sie do kogos

Eta: Dzięki za info......... nie załapałam,bo ...... jestem" starej daty"

b.: a ja widze, ze cos usuwalem i wyszlo bez sensu, co napisalem, no ale juz trudno

Keira: Eta − w zad. 1. zatrzymalam się w pewnym momencie: n∊N, k∊N 2ⁿ + 1 =k² 2ⁿ=k² − 1 = (k + 1)(k−1) k−1>0, k>1 2ⁿ − l. parzysta, zatem (k + 1) i (k−1) to l. parzyste Pierwsza para, która pasuje to 4 i 2, n = 3. Ale nie wiem jak sprawdzić pozostałe pary.

think: Keira zastanawiam się, czy np gdybyś sobie narysowała wykres funkcji f(x) = 2ⁿ i g(x) = k² − 1, to może udałoby Ci się ten dylemat zażegnać graficznie znaczy to jest wykres dyskretny czyli punktowy ale i tak dużo to pewnie da

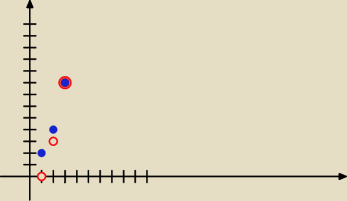
think: f(x) = 2^x g(x) = x² − 1 tak miało być

Eta: Keira Wszystko ok (k+1) i (k−1) parzyste, są potęgami dwójki i odległe od siebie o 2 więc tylko taki warunek spełniają 4 i 2 bo np; 8 i 16 są potęgami dwójki, ale ich odległość od siebie jest 8 czyli odpadają itd...... zatem n= 3

Keira: aahaa, ale dlaczego k+1 i k−1 muszą być potęgami dwójki Podejrzewam, ze inaczej nie wyjdzie 2 do potęgi, ale to jest jakaś własność czy coś

Keira: a sposób THINK też ciekawy

Eta: No tak bo masz otrzymać 2ⁿ 2ⁿ = ( k+1)(k−1) ....... to chyba oczywiste bo 6* 4= 2³*3≠2ⁿ czyli mało,że muszą być parzyste ....... muszą być potęgami 2 i dodatkowo odległość między nimi wynosi 2 bo są postaci: ( k−1 , k+1)

think: no ale tam potrzebna jest wiedz typu że funkcja wykładnicza szybciej śmiga w górę niż potęgowa i dlatego, rozwiązanie będzie tylko to jedno ale dowiesz się wszystkiego w swoim czasie wiesz mi zawsze sprawiało swoistą frajdę, gdy poznawałam nowe 'możliwości' matematyki, odkrywanie, że zadanie, które robiło się strasznie długo jakąś metodą można zrobić tą nowo poznaną znacznie szybciej a czasem o zgrozo wystarcza do tego znacznie mniej danych a teraz zmykam do jutra

Eta: Bardzo obrazowo [Pthinki]] to przedstawiła Takim sposobem widzisz punkty wspólne dla wykresów obydwu funkcjii Widać wyraźnie,że innych punktów już nie ma, bo parabola i krzywa wykładnicza dalej już się "rozjeżdżają"

Eta: Dobranoc Lucynko

Keira: taak, dziękuję

Godzio:

b.: uściślę nieco, jeśli 2ⁿ= (k + 1)(k−1) to (k+1) oraz (k−1) są dzielnikami 2ⁿ, więc są potęgami dwójki (2ⁿ ma w rozkładzie na czynniki pierwsze tylko dwójki, więc również k+1 i k−1, jako dzielniki 2ⁿ, muszą mieć tę własność) samo z siebie nie oznacza to jednak, że k−1 i k+1 są parzyste, bo 2⁰=1 też jest potęgą dwójki jeden ze sposobów na formalne uzasadnienie, czemu jedynym rozwązaniem jest k=3: mamy k−1 = 2^p, k+1=2^q, więc p<q, odejmując stronami: 2 = 2^q − 2^p 2 = 2^p(2^q−p−1) i stąd widzimy, że 2^p dzieli liczbę 2, więc p=0 lub p=1, i te dwa przypadki można już sprawdzić ,,ręcznie''

Keira: Mhm, wszystko jasne

b.: I zostaly jeszcze dwa drugie zadania